钛酸锂电池凭借着出色的功率性能和优异的循环寿命，在动力锂离子电池领域得到了一席之地，在一些对快充和低温性能要求较高的领域得到了应用。等效电路模型是模拟锂离子在放电过程中电压和温度变化的有效工具，但是传统的等效电路模型在较宽的电流和温度范围内，拟合效果并不理想。

 

       近日，北京交通大学的AnciChen（第一作者）和Weige Zhang（通讯作者）、Caiping Zhang（通讯作者）等人通过将修正Bulter-Volmer公式和Nernst公式应用在等效电路模型之中，从而使得等效电路模型适应了不同温度和电流范围，从而显著提升了仿真精度。

 

       钛酸锂电池在使用过程中通常会面临大电流的使用工况，会导致电池温度在较大的范围内波动，因此对电池更为准确的模拟需要充分考虑温度和电流的相互影响。通常锂离子电池的模型可以分为三大类:1）电化学模型；2）数学模型；3）等效电路模型。电化学模型能够根据电池内部的反应机理对电池的充放电行为进行模拟，但是这一模型的复杂程度较高。对于数学模型而言，通常是借助经验公式或数学方法获得电池的模型，但是这种方法中的参数缺少准确的物理含义，因此模拟的准确度较低。等效电路模型则是采用各种元器件模拟电池电流和电压，从而实现在较少的参数的前提下，获得较高的拟合准确度。

 

       为了提升等效电路对温度和电流的适应性，常见的办法时建立一个随温度和电流变化的参数查询表，但是这种方法缺少理论依据，因此参数表的准确性对模型准确性会产生显著的影响。为了提升模型的准确性，人们尝试将等效电路的参数在理论的基础上建立与温度和电流的关系，例如Zhu等人就通过阿伦尼乌斯公司对Butler-Volmer公式进行修正，从而建立了电荷交换阻抗与温度和电流之间的关系，但是这种方法的误差较大。

 

       在该项研究中作者采用了传统的等效电路模型的基础上，考虑了温度和电流对于模型参数的影响，作者对BV等式进行了修正和简化，然后整合到了整个模型之中，同时为了反映温度对于开路电压的影响，作者在等效电路模型中引入了Nernst公式。采用多项式修正的方法对温度对电池欧姆阻抗的影响进行了分析。

 

       电池的等效电路模型通常可以根据两种机理构建，一种时基于交流阻抗构建的等效电路，能够模拟电池对频率的响应特征，但是对直流的响应的模拟并不好，同时计算的复杂程度还比较高。另外一种时基于Thevenin的等效电路模型（如下图所示），其中包含一个电压源，R0则主要反应电极、电解液和隔膜的欧姆阻抗，而RC并联电路主要用来反应电极的电池极化和动力学特性。

 

       在这里作者采用了1维的等效电路，这主要是因为1维模型的就能够对电池的行为进行较为准确的模拟，其次是这种模型能够更为准确的对高功率电池进行模拟。

       为了能够分析SoC、温度、电流和电流方向对于电路参数的影响，作者引入了能斯特方程等原理。

 

       Ⅰ能斯特方程

 

       电池的电压主要反应电池储存的能量，受到温度的影响，根据能斯特方程电池的开路电压与温度的关系如下式所示，其中R为气体常数，T为绝对温度，z电化学反应交换的电子数，F为法拉第常数，Q为反应物的比例（在这里作者认为电池内部的反应物的浓度变化可以忽略，因此Q为定值），值得注意的是下式中的参数都与温度无关，但是与电池的SoC状态密切相关。

      Ⅱ BV公式的再修正

 

       BV公式是最重要的电化学动力学公式，主要描述了电流密度与稳态过电势之间的关系（如下式所示），其中j为电流密度，j0为交换电流密度，α为对称系数，ηmax为稳态电化学过电势。

       上述公式仅能够在固定的温度下使用，因为交换电流密度j0与温度之间存在密切的关系，根据交换电流密度的定义，作者给出了如下所示的交换电流密度的定义公式，其中Aa为常数项，[R]表征反应物的浓度，φe表征电极的电势，Ea0则表征反应的活化能，

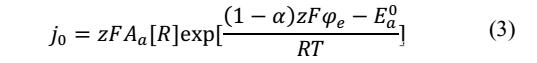
       根据Nernst公式，φe可以采用下式4进行表征，Ea0则可以通过下式5表征为温度的函数，m为一个无关温度的常数。

       开路电压可以用下式进行表征

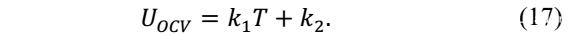
   电池的电流密度可以根据电池的电流和有效面积求得

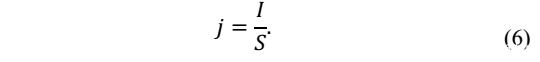
       根据上面的推断，BV方程则可以转化为如下式7所示的形式，研究表明对称系数α在实际中基本上都在0.5附近，很少变化，对公式7进行求解，结果如下式8所示的形式。下式8中所有的参数都与温度和电流无关，仅与电池的SoC有关，因此我们可以根据公式8对电池对电池在不同的电流和温度下的电压特性进行模拟。

       由于在上式8中所有的参数都仅与SoC状态有关，因此该模型可以进一步简化为下式

 

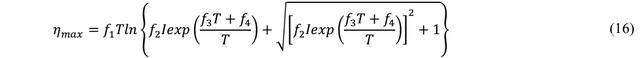
       电池欧姆阻抗基本不受电池电流的影响，但是却受到温度的显著影响，但是研究表明欧姆阻抗R0受温度影响的规律并不符合阿伦尼乌斯公式，因此作者在这里采用了一个多项式描述欧姆阻抗受到温度的影响（如下式所示），其中P1、P2和P3分别多项式的系数

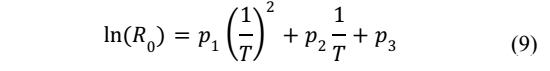
       测试系统如下所示，包含测试设备、恒温箱和电池，电池的基本信息如下表所示

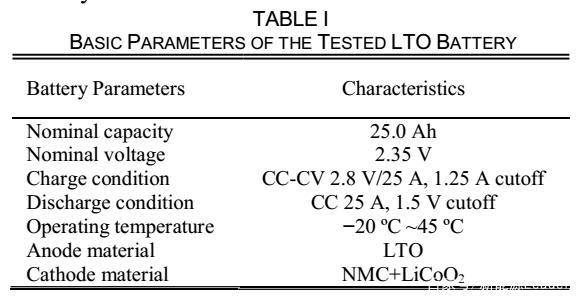
       首先作者测试了电池的容量，具体步骤为采用CC-CV制度对电池进行充电，然后以1C倍率下进行放电，以测量电池的容量，重复该过程3次，以得到平均电池容量。然后作者分别在5℃、15℃、25℃和45℃测试了电池在10%-90%SoC范围内，电池的开路电压和欧姆阻抗。然后作者采用FUDS测试（如下图所示）验证了模型的准确性。

       该模型的整体运行流程如下图所示，其中修正后的BV公式能够为模型提供不问温度和电流下的极化信息，Nernst公式则可以用来描述不同温度下的开路电压特征。

 

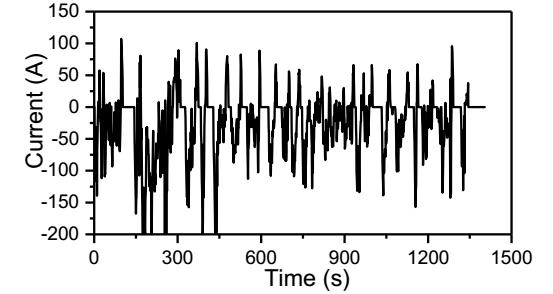
       实验中作者将电池的工作定义为电池在给定的SoC和温度T下首先以电流I（正为充电，负为放电）工作时间t，然后静置t1时间，因此电池的SoC状态可以通过下式积分求得，其中Cap为25℃条件下电池在1C倍率下的放电容量。

 

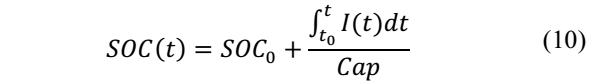
       因此模型中与SoC相关的参数可以表述为下式

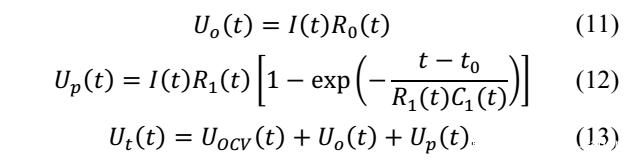
       在静置条件下电池的开路电压可以用下式进行描述，在模型中作者对于电容C的数值没有进行专门的设计，这主要是因为电容C的数值对于模型准确性的影响较小，因此作者将RC并联电路的时间常数固定在15s。模型中与SoC相关的参数1, 2, 3, 1, 2, 3, 4, 1 2则是根据最小二乘法拟合利用线性插值的方式获得。同时由于作者假设忽略浓差极化的影响，但是在充放电末期时浓差极化较为显著，因此不能不忽略，因此该模型仅适合模拟电池在10%-90%SoC范围内电池的行为。

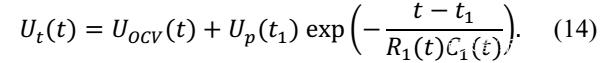
       等效电路模型的首先要做的工作就是确定电池的开路电压，下图中展示了快速测量钛酸锂电池开路电压的方法，电池以1C倍率进行充放电，每5%SoC电池静置5min，然后根据充电和放电电压作者得到了下图中绿线所示的开路电压曲线。

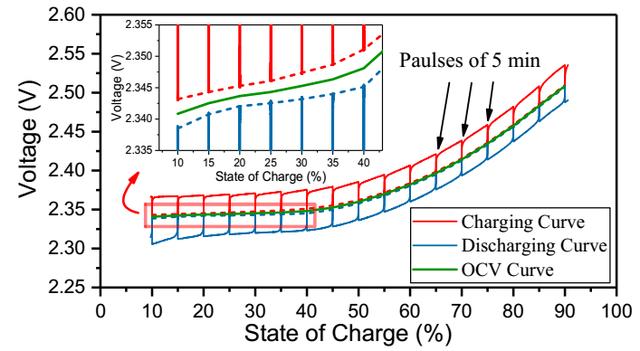
       接下来作者分别测试了在5℃、15℃、25℃和45℃下的开路电压，如下图所示

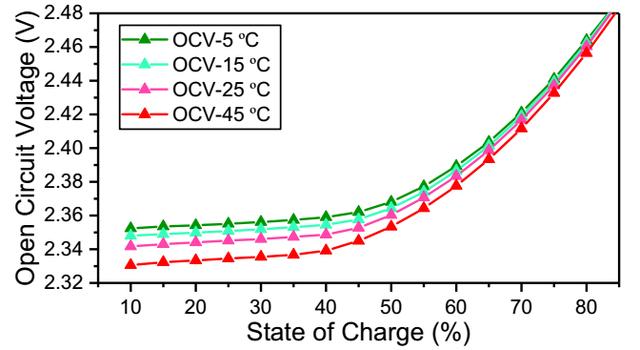
       在下图中作者分别根据Nernst方程计算了电池在10%、45%和80%SoC状态下电池的开路电压与温度之间的关系，可以看到计算结果与实际结果符合的非常好。

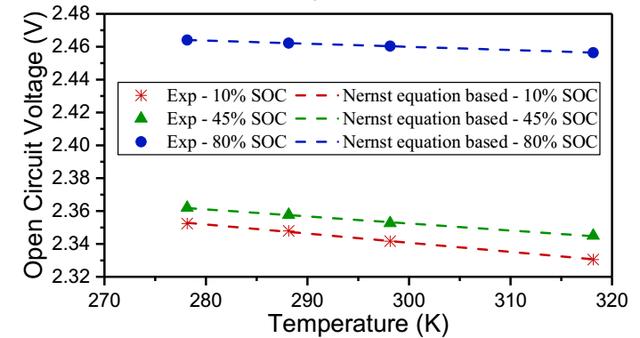
       下图为电池在放电过程中静置期间的电压变化，我们可以根据电流变化瞬间引起的压降计算电池的欧姆阻抗（如下式所示），这里两次取样时间的间隔设定为1s，这主要是因为电池的极化通常需要数十秒，甚至是数百秒的时间达到平衡，因此在1s的时间内电池的极化不会发生显著的变化，因此此时的电压变化主要来自于电池的欧姆阻抗。

       下图为作者根据阿伦尼乌斯公式绘制的在特定的SoC状态下电池的欧姆阻抗与温度之间的关系，从图中能够看到两者呈现非线性的关系，这表明欧姆阻抗与温度之间并不遵循阿伦尼乌斯公式，因此作者在这里采用一个多项式对电池的欧姆阻抗与温度之间的关系进行了描述，从同种能够看到拟合结果与实测结果之间符合的非常好。

       在上面我们已经获得了电池的开路电压和欧姆阻抗R0，因此我们可以根据上式16来计算电池的稳态极化电压，在这里作者采用了恒流充电过程中的数据，以确保电池的极化达到稳态。下图分别为电池在不同的温度下以不同的电流进行充放电的极化电压数据，从图中能够看到温度和电流对于电池开路电压的影响是呈现非线性的关系，作者在这里采用修正的BV公式获得了拟合结果，从图中能够看到仿真结果与实测结果最大误差约为2.2mV。

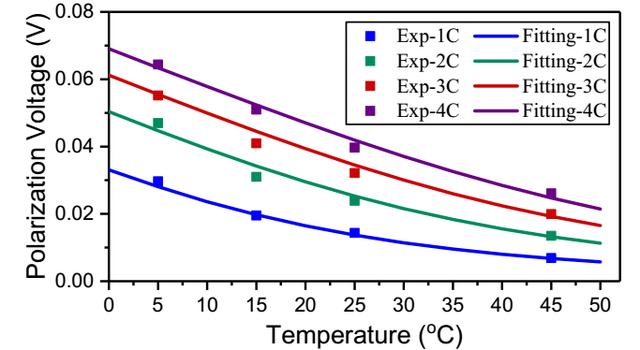
       为了进一步验证模型的有效性，作者采用在不同温度下4C恒流充放电的形式对电池进行了测试，从下图a的充电工况模拟结果可以看到，在前516s中拟合误差在0.2%以内，在516s后误差也控制在-0.2%至0.5%之间，仅在5℃下误差增长较快达到3.5%，这主要是受到低温下电池较低的传质速率的影响，因此浓差极化的影响不能再被忽略，导致误差升高。

 

       下图b则展示了在不同温度下的4C放电数据，从图中能够看到在整个放电过程中，不同温度下模型拟合的结果都非常好，误差都在0.8%以内。

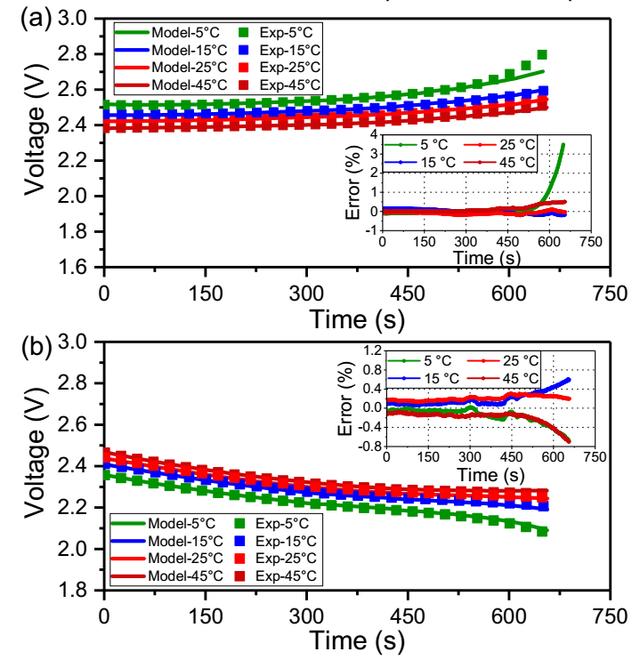
       接下来作者采用更为复杂的FUDS制度对模型的准确性进行了检验，电池的最大电流可以达到8C左右，从下图a中可以看到即便是在如此复杂的使用工况中，模型对于电压预测的最大误差也仅为-4%与1.7%之间，从下图c中可以看到在35℃的条件下模型能够获得更好的预测精度，误差仅为-0.7%至0.3%之间，这主要是因为高温下良好的传质速率，消除了浓差极化造成的影响。

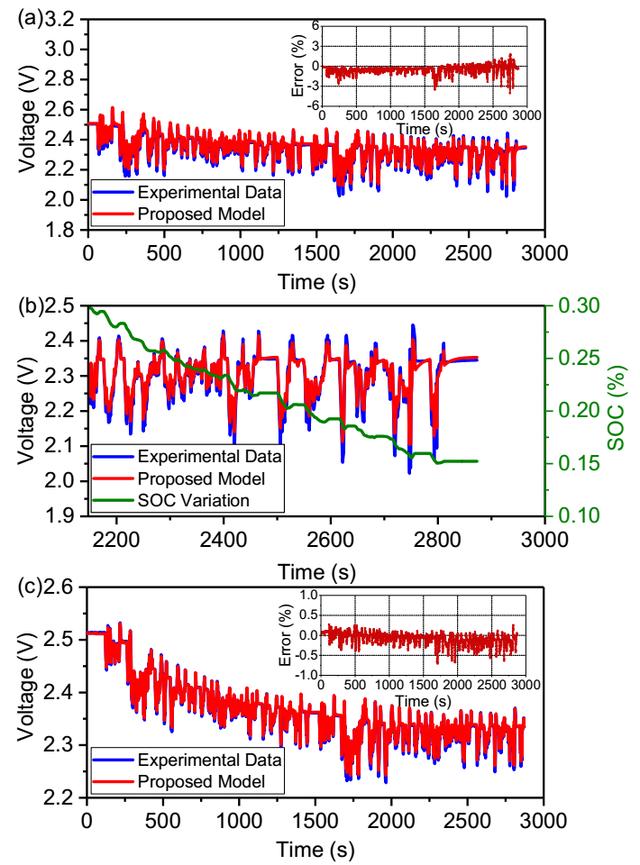
       下图中作者对比该修正后等效电路模型与传统的等效电路的模拟效果，当电池在1C倍率放电和5℃的条件下，传统的等效电路模型的误差要明显的高于修正后的等效电路模型，传统的等效电路模型的误差为-14.86mV至-28.68mV之间，而修正后的模型的电压误差则仅为-3.68mV至4.45mV之间。

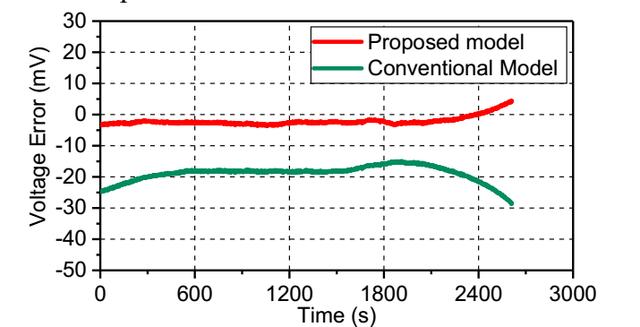
       下图作者对比了常温下，4C倍率放电时两种等效电路模型的误差范围，从图中能够看到传统的等效电路模型的电压误差在8.09mV至21.55mV之间，而修正后的等效电路模型小于6.94mV。

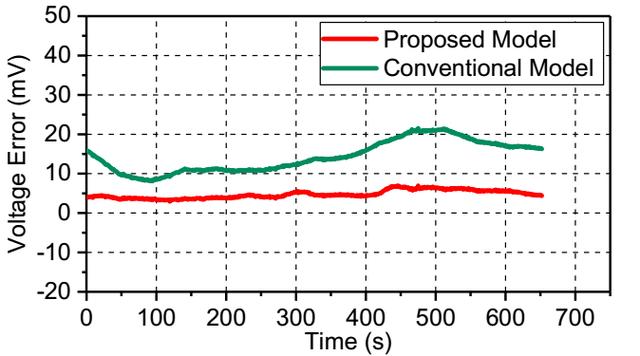
       下图为作者在5℃下采用FUDS循环对模型预测电池SoC状态预测的结果，其中第一种方法时基于修正后的等效电路模型，以及卡尔曼滤波函数，第二种方法时基于传统的等效电路模型和卡尔曼滤波函数，第三种方法是基于一维等效电路模型和双卡尔曼滤波函数。从下图的预测结果可以看到第一种和第三种方法都取得了较高的预测精度，其中第一种方法的误差为-0.99%至3.02%，第三种方法的预测误差在-1.13%至1.51%，而第二种放大的误差则达到了5.34%至11.6%之间，三种方法的平均误差分别为1.82%、9.89%和0.68%，可以看到修正的等效电路模型对于SoC状态的预测取得了较高的精度。

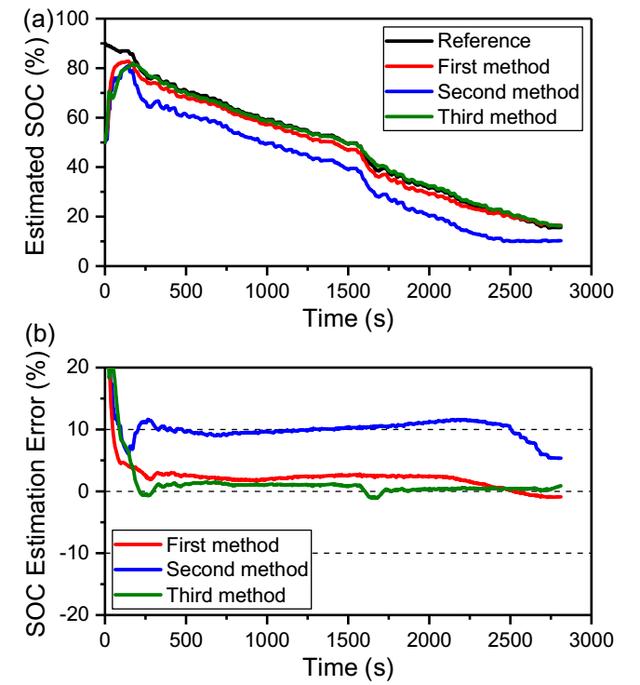
       Anci Chen通过利用能斯特方程和阿伦尼乌斯方程等工具，将温度和电流对于电路参数的影响引入了一维等效电路模型，从而大大提升了模型预测的准确度。